Форма следует за функцией

Способы задания функции

Функция — это зависимость «y» от «x», где «x» является переменной или аргументом функции, а «y» — зависимой переменной или значением функции.

Задать функцию значит определить правило, в соответствии с которым по значениям независимой переменной можно найти соответствующие ее значения. Вот, какими способами ее можно задать:

• Табличный способ — помогает быстро определить конкретные значения без дополнительных измерений или вычислений.
• Графический способ — самый наглядный. На графике сразу видно возрастание и убывание функции, наибольшие и наименьшие значения, точки максимума и минимума.
• Аналитический способ — через формулы. Компактно, и можно посчитать функцию при произвольном значении аргумента из области определения.
• Словесный способ.

Нужно быстро привести знания в порядок перед экзаменом? Записывайтесь на курсы ЕГЭ по математике в Skysmart!

Понятие функции

Определение функции можно сформулировать по-разному. Рассмотрим несколько вариантов, чтобы усвоить наверняка.

1. Функция — это взаимосвязь между величинами, то есть зависимость одной переменной величины от другой.

Знакомое обозначение y = f (x) как раз и выражает идею такой зависимости одной величины от другой. Величина у зависит от величины х по определенному закону, или правилу, которое обозначается f.

Вывод: меняя х (независимую переменную, или аргумент) — меняем значение у.

2. Функция — это определенное действие над переменной.

Значит, можно взять величину х, как-то над ней поколдовать — и получить соответствующую величину у.

В технической литературе можно встретить такие определения функции для устройств, в которых на вход подается х — на выходе получается у. Схематично это выглядит так:

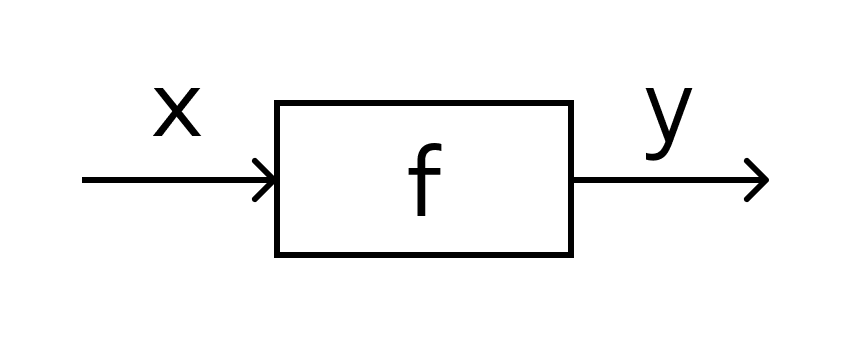
В этом значении слово «функция» используют и в далеких от математики областях. Например, так говорят о функциях ноутбука, костей в организме или даже о функциях менеджера в компании. В каждом перечисленном случае речь идет именно о неких действиях.

3. Функция — это соответствие между двумя множествами, причем каждому элементу первого множества соответствует один элемент второго множества. Это самое популярное определение в учебниках по математике.

Например, функция у = 2х каждому действительному числу x ставит в соответствие число y, которое в два раза больше, чем х.

Область определения — множество х, то есть область допустимых значений выражения, которое записано в формуле.

Например, для функции вида

область определения выглядит так:

х ≠ 0 (потому что на ноль делить нельзя)

И записать это можно так: D (y): х ≠ 0.

Область значений — множество у, то есть это значения, которые может принимать функция.

Например, естественная область значений функции y = x2 — это все числа больше либо равные нулю. Можно записать вот так: Е (у): у ≥ 0.

Для примера рассмотрим соответствие между двумя множествами — человек-владелец странички в инстаграм и сама страничка, у которой есть владелец. Такое соответствие можно назвать взаимно-однозначным — у человека есть страничка, и это можно проверить. И наоборот — по аккаунту в инстаграм можно проверить, кто им владеет.

В математике тоже есть такие взаимно-однозначные функции. Например, линейная функция у = 3х +2. Каждому значению х соответствует одно и только одно значение у. И наоборот — зная у, можно сразу найти х.

Рассмотрим другие типы соответствий между множествами.

Например, фрукты и цвет каждого:

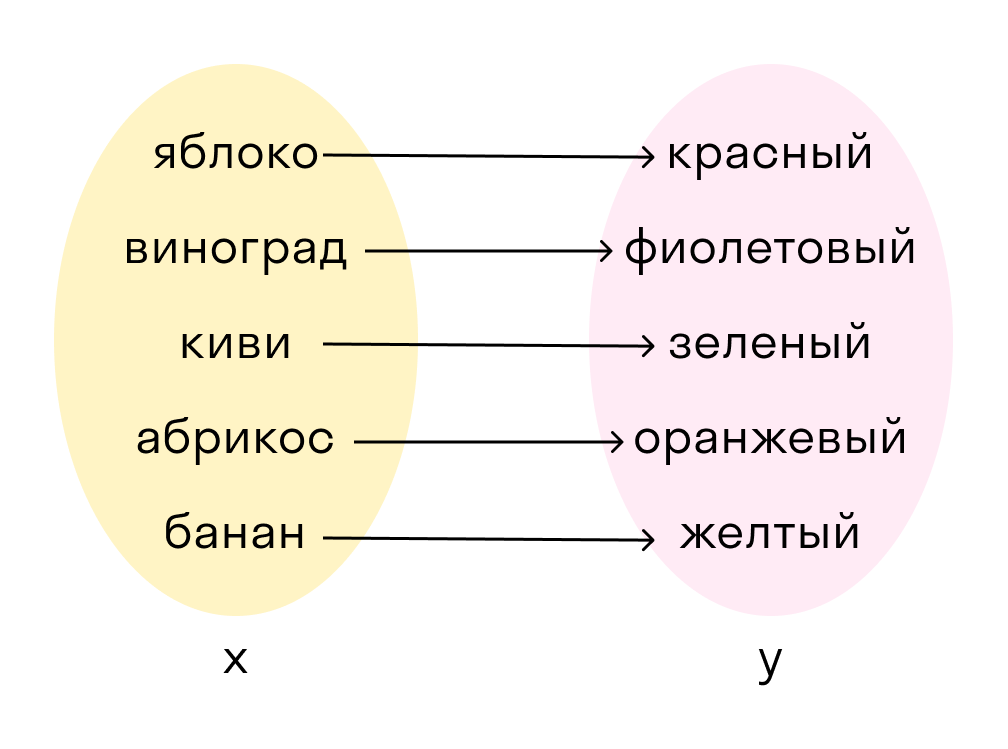
У каждого фрукта есть свой цвет. Но такое соответствие нельзя назвать взаимно-однозначным. Например, яблоко может быть и красным, и желтым и даже зеленым.

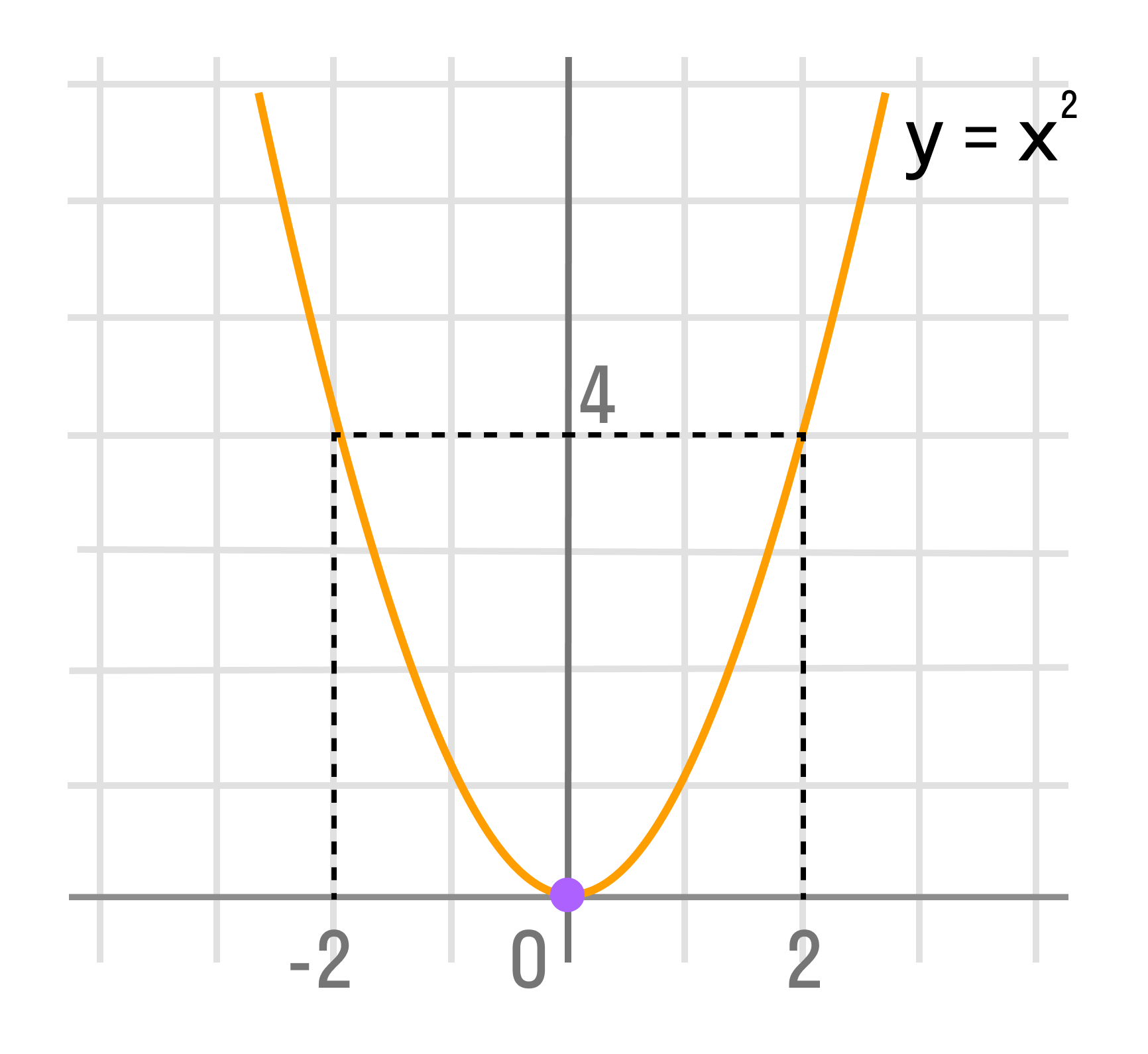
Пример такого соответствия в математике — функция у = х2. Один и тот же элемент второго множества у = 4 соответствует двум разным элементам первого множества: х = 2 и х = -2.

Так на примере с фруктами можно показать соответствие, которое нельзя назвать функцией:

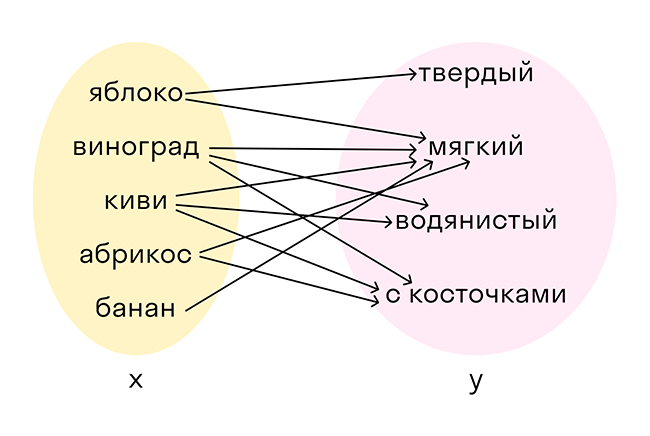
Видно, что в первом множестве есть элементы, которым соответствует два или три элемента из второго множества. Описать такое соответствие математически было бы сложнее.

Задать функцию графиком

График функции — это объединение всех точек, когда вместо «x» можно подставить произвольные значения и найти координаты этих точек.

График функции показывает множество всех точек, координаты которых можно найти, просто подставив в функцию любые числовые значения вместо «x».

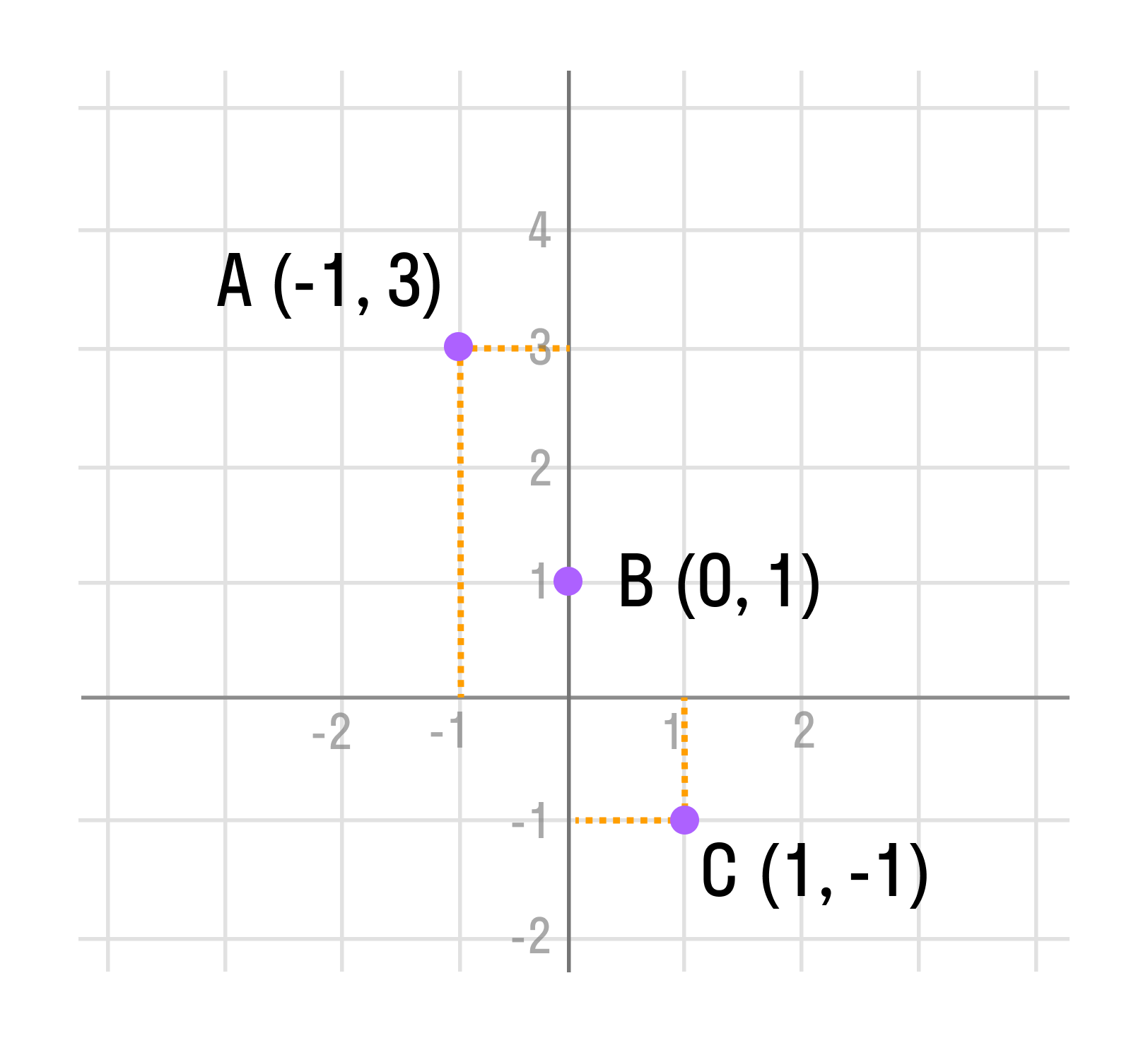
Пример. Дана функция: y(x) = −2x + 1.

Найти: значения «y» для произвольных «x», а именно −1, 0, 1.

Как рассуждаем:

1. Подставим данные значения х в функцию и запишем результаты:

2. Каждая пара значений «x» и «y» — это координаты точек по оси Ox (абсцисса точки) и Oy (ордината точки).

Дадим названия каждой точке и запишем их координаты:

3. Отметим точки А (-1; 3), B (0; 1) и С (1; -1) на прямоугольной системе координат.

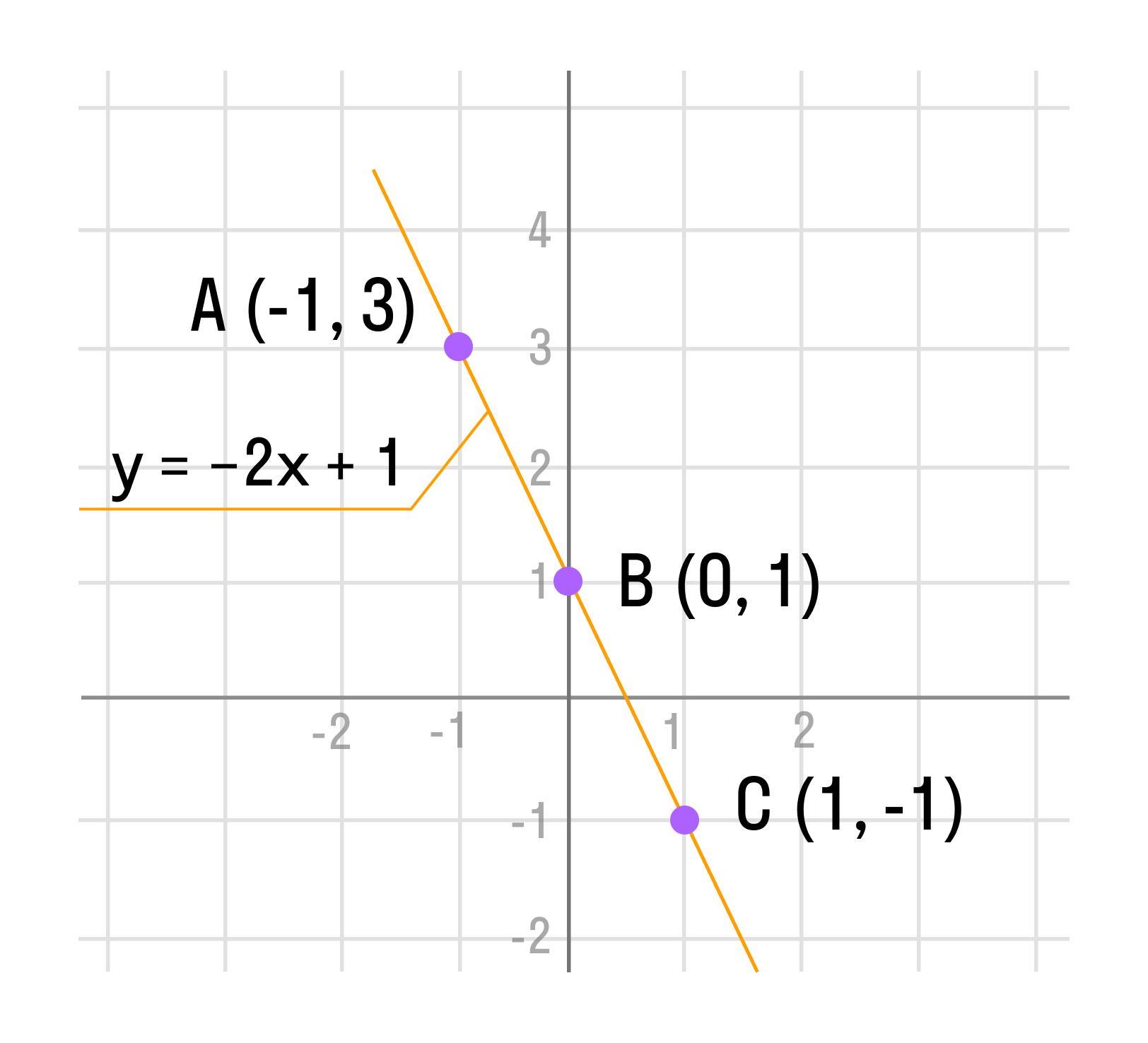
4. Соединим отмеченные точки прямой.

Проведенная прямая будет графиком функции y(x) = −2x + 1.

Форма

«Все вещи в природе имеют форму, — сказал Салливан, — то есть форму, внешнее подобие, которое говорит нам, что они собой представляют, что отличает их от нас самих и друг от друга». То, что эти формы «выражают внутреннюю жизнь» вещи, — это закон природы, которому следует следовать в любой органической архитектуре. Салливан предполагает, что внешняя «оболочка» небоскреба должна измениться по внешнему виду, чтобы отражать внутренние функции. Если эта новая органическая архитектурная форма должна была стать частью естественной красоты, фасад здания должен изменяться по мере изменения каждой внутренней функции.

Расцвет небоскребов

Небоскреб был новым в 1890-х годах. Более надежная сталь, полученная по бессемеровскому процессу, может использоваться для столбов и балок. Прочность стального каркаса позволила зданиям быть выше без толстых стен и аркбутанов. Эта структура была революционной, и архитекторы Чикагской школы знали, что мир изменился. США после Гражданской войны изменились с сельской на городскую, и сталь стала строительным материалом для новой Америки.

Основная сфера применения высоких зданий — офисная работа, побочный продукт промышленной революции — была новой функцией, которая требовала новой городской архитектуры. Салливан понимал как масштабы этого исторического изменения в архитектуре, так и возможность того, что красота может быть оставлена ​​позади в стремлении стать самым высоким и новейшим. «Дизайн высокого офисного здания занимает свое место среди всех других архитектурных типов, созданных, когда архитектура, как это бывало однажды за много лет, была живым искусством». Салливан хотел построить красивые здания, такие как греческие храмы и готические соборы.

Он решил определить принципы дизайна в своем эссе 1896 года: ’»Высокое офисное здание с художественной точки зрения», опубликованное в том же году, когда здание Prudential Guaranty Building выросло в Буффало. Наследие Салливана — помимо внушения идей своему молодому ученику, Фрэнку Ллойду Райту (1867-1959) — было документированием философии дизайна для нескольких -Используйте здания.Салливан выразил свои убеждения словами, идеи, которые продолжают обсуждаться и обсуждаться сегодня.

Происхождение фразы

Архитектор Луи Салливан придумал максиму , хотя ее часто неправильно приписывают скульптору Горацио Гриноу (1805–1852), чье мышление в основном предшествовало более позднему функционалистскому подходу к архитектуре. Сочинения Гриноу на долгое время были в значительной степени забыты и были заново открыты только в 1930-х годах. В 1947 году подборка его эссе была опубликована как « Форма и функция: примечания к искусству» Горацио Гриноу .

Салливан был гораздо более молодым соотечественником Гриноу и восхищался такими мыслителями-рационалистами, как Торо , Эмерсон , Уитмен и Мелвилл , а также самим Гриноу. В 1896 году Салливан придумал эту фразу в статье под названием «Высокое офисное здание, рассматриваемое с художественной точки зрения» , хотя позже он приписал основную идею римскому архитектору, инженеру и писателю Маркусу Витрувиусу Поллио , который впервые в своей книге « Архитектура» утверждал, что сооружение должно проявлять три качества фирмит, утилит и венуст, то есть быть прочным, полезным, красивым. Салливан на самом деле писал «форма всегда следует за функцией», но более простая и менее выразительная фраза запоминается более широко. Для Салливана это была чистая мудрость, эстетическое кредо, единственное «правило, которое не допускает никаких исключений». Полная цитата:

Будь то стремительный орел в его полете или распустившийся яблоневый цвет, трудящаяся рабочая лошадь, веселый лебедь, ветвящийся дуб, извилистый ручей у его основания, плывущие облака над всем бегущим солнцем, образуют вечную форму. следует функции , и это закон. Там, где функция не меняется, форма не меняется. Гранитные скалы, вечно задумчивые холмы остались на века; молния живет, принимает форму и умирает в мгновение ока.

Это всепроникающий закон всего органического и неорганического, всего физического и метафизического, всего человеческого и всего сверхчеловеческого, всех истинных проявлений головы, сердца, души, в которых жизнь узнаваема. его выражение, эта форма всегда следует за функцией. Это закон.

Салливан разработал форму высокого стального небоскреба в Чикаго в конце 19-го века в момент, когда сошлись технологии, вкусы и экономические силы, и возникла необходимость нарушить устоявшиеся стили. Если форма здания не должна была выбираться из старой книги образцов, что-то должно было определять форму, и, по словам Салливана, это должно было быть предназначением здания. Таким образом, «форма следует за функцией», в отличие от «форма следует за прецедентом». Помощник Салливана Фрэнк Ллойд Райт принял и исповедовал тот же принцип в несколько иной форме — возможно, потому, что отказ от старых стилей дал им больше свободы и свободы действий.

Архитектор Луи Салливан

Луи Салливан (1856-1924), родившийся в Бостоне, штат Массачусетс, стал пионером американского небоскреба в основном на Среднем Западе, создав «салливанский» стиль, который изменил облик архитектуры. Салливан, одна из величайших фигур в американской архитектуре, повлиял на язык стиля архитектуры, который характеризовал то, что стало известно как Чикагская школа.

Салливан, которого часто называют первым по-настоящему современным архитектором Америки, утверждал, что внешний дизайн (форма) высокого здания должен отражать действия (функции), которые происходят внутри его стен, представленных механическим оборудованием, магазинами розничной торговли и офисами. Его здание Уэйнрайт 1891 года в Сент-Луисе, штат Миссури, является культовой демонстрацией философии и принципов дизайна Салливана

Обратите внимание на терракотовый фасад этого раннего высотного здания со стальным каркасом: нижние этажи требуют иной конфигурации окон с естественным освещением, чем центральные семь этажей внутренних офисных помещений и верхний чердак. Трехчастная архитектурная форма Wainwright похожа на более высокое здание Prudential Guaranty Building 1896 года, построенное партнерами Адлера и Салливана в Буффало, штат Нью-Йорк, аналогичной формой, потому что эти структуры имели аналогичные функции

Примечания и ссылки

1. Horatio Greenough, Form and Function: Remarks on Art , под редакцией Гарольда А. Смолла (Berkeley, Univ. of California Press, 1947), хотя теория неотъемлемых форм, краткое изложение которой представляет собой эта фраза, информирует обо всех работах Гриноу. писать об искусстве, дизайне и архитектуре. В своих архитектурных работах Гриноу находился под влиянием трансценденталистского мышления и унитарного протестантизма Ральфа Уолдо Эмерсона .
2. Салливан, Луи Х. (1896). . Исследовательский институт Гетти .
3. . Нью-Йорк: издательство Американского института архитекторов, Inc., 1924. с. 108.
4. Салливан, Луи Х. (1896). . Журнал Липпинкотта (март 1896 г.): 403–409.
5. Лоос, А. (1908). . Вена.
6. Джеффри Мейкл «Twentieth Century Limited: промышленный дизайн в Америке, 1925–1939»
7. Спинеллис, Диомидис (май 2008 г.). . ICSE ’08: Материалы 30-й Международной конференции по программной инженерии . Лейпциг, Германия: Ассоциация вычислительной техники. стр. 381–390. DOI. Проверено 19 октября 2011 г. .
8. . Автомобильные новости . Проверено 08 января 2018 г. .