Александр волошинов: математика и искусство

Парадокс Банаха-Тарского

slavikap-2.livejournal.com

Парадокс был открыт в 1926 году математиками Стефаном Банахом и Альфредом Тарским и заключается в следующем: если разбить шар на куски, то можно собрать два таких же шара. На практике это невозможно, но в теории очень даже. «В некотором смысле это настоящее волшебство», – подчеркивает Бриц.

Перечисленные понятия – лишь малая часть всей красоты математики. «Чтобы замечать больше, необходимы базовые знания и постоянная практика, – отметил Томас. – Требуется утомительная подготовка, как и спортсменам, которые вынуждены тренироваться снова и снова. Но это того стоит. Я надеюсь, математику полюбят больше людей, ведь в ней полно скрытой красоты».

5 примеров «красоты математики».

«Правильный взгляд на математику открывает не только истину, но и безупречную красоту…», – писал британский математик и философ Бертран Рассел. Математические явления можно встретить в природе повсеместно: раковину наутилуса, символизирующую золотое сечение, речные потоки и морские побережья фрактальной формы и многое другое.

Томас Бриц, преподаватель кафедры математики и статистики в Университете Нового Южного Уэльса (Австралия), с детства увлекается математикой и уверенно утверждает, что в повседневной жизни можно встретить как минимум 5 вещей, которые доказывают, что математика подобна искусству.

Геометрия в дизайне интерьера

Геометрия как наука возникла очень давно и в своей сущности она означает одно — пространственное воображение, подчиненное логике. Перспектива — одно из таких геометрических направлений, которая развивалась в двух направлениях. Первое — архитектура, строительство, дизайн, техника и второе — живопись.

Египетские пирамиды, Парфенон, многие древние храмы, Колизей были построены на основе изображений (прототипов чертежей), которые были тщательно рассчитаны и распланированы.

Последовательность Фибоначчи

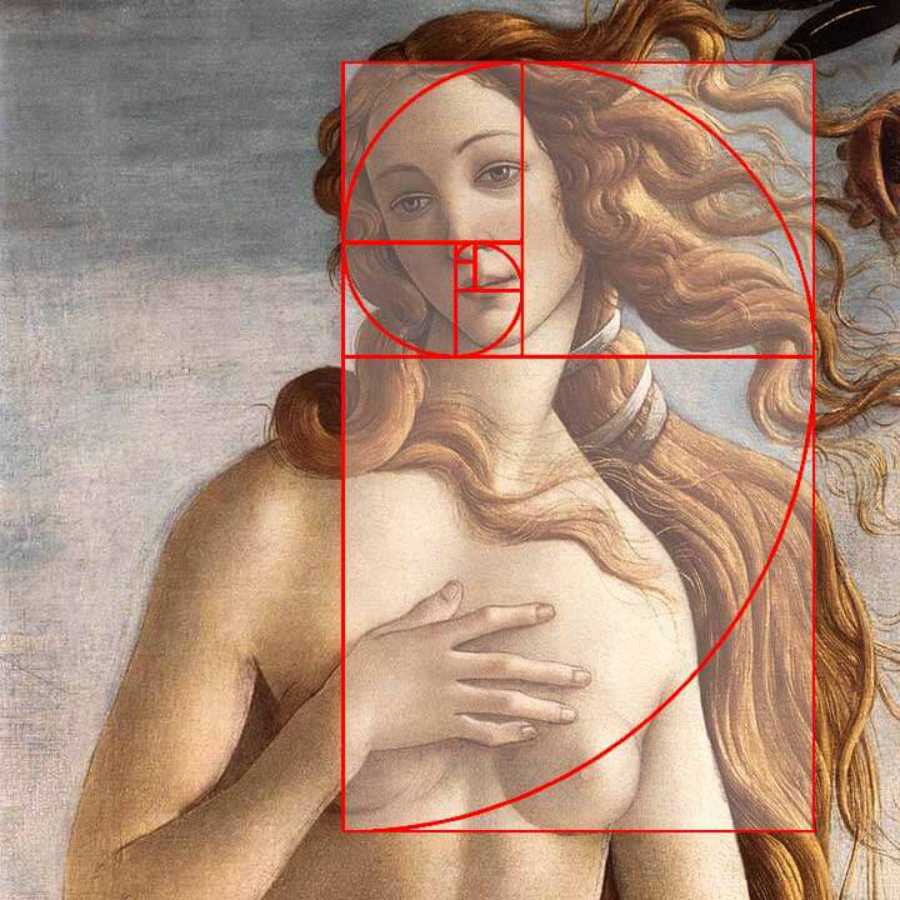
Многие ли из вас слышали о последовательности Фибоначчи? Это ряд чисел: 1, 2, 3, 5, 8, 13, 21, 34, 55… Каждая из цифр в этом ряду является суммой двух предыдущих и играет значительную роль в дизайне. Если представить себе эти числа в виде квадратов 1 х 1…. 55 х 55…, то сочетания этих квадратов можно использовать для формирования так называемого золотого прямоугольника. Соотношения между двумя соседними числами по смыслу приближено к золотому сечению.

Золотое сечение

Кстати, о так называемом золотом сечении (золотой пропорции, золотом соотношении). Правило золотого сечения (это такое пропорциональное деление отрезка на неравные части, при котором меньший отрезок так относится к большему, как больший к меньшему a: b= b : c или с : b= b : а)…

…применялось практически во всей древнегреческой и древнеримской архитектуре и считалось эталоном измерения.

 

Золотое соотношение описывает гармоничную зависимость между шириной и высотой. В мире нет ничего случайного, и этот математический принцип (как, впрочем, и все остальное) взят людьми явно из природы.

Золотое соотношение и последовательность Фибоначчи использовали не только в архитектуре, но и в живописи. Как пример — Мона Лиза Леонардо да Винчи. Гармония была залогом долговечности древних построек и красоты картин.

Графическая тетрадь «Математика — это красиво!» Анна Вельтман

Мои постоянные читатели знают, почему я не смогла бы оставить без внимания книгу, а вернее, графическую тетрадь с названием «Математика — это красиво!» : )

Как я уже писала:

И это только то, что мне в тот раз удалось вспомнить навскидку о графической стороне этой величайшей науки.

Моя коллега Анна Вельтман, учитель математики из США, в этой книге постаралась собрать самые интересные подтверждения этого, а также того, что математика является основой окружающего нас мира, в том числе основой изобразительного искусства. Анна приглашает желающих убедиться в этом на собственном опыте — предложенные графические задания можно выполнять в этой же тетради.

Рисование математических повторяющихся узоров увлекает, завораживает и оказывает расслабляющее действие, недаром многие дети рисуют их на уроках (а взрослые — на совещаниях). Примеры таких узоров и орнаментов есть в книге.

Чем еще удивительна эта книга? Она покажет ребенку не только красоту математики, но и ее волшебство: то, что…

С ней ребенок научится создавать:

• поворотную мозаику
• рисунки числами
• рисунки пиксельными картинками
• трехмерные рисунки
• оптические иллюзии: невероятные треугольники и невероятные звезды
• головоломки-раскраски
• фрактальные узоры и снежинки Коха
• многое другое

В конце тетради есть еще глоссарий (словарик математических терминов) и идеи для других занятий, в том числе помимо рисования: идеи создания поделок из ниток, витражных красок и других материалов на основе рисунков, выполненных по заданиям из этой тетради. А также несколько листов, разлинованных по-разному и разными цветами — для воплощения идей из книги или своих собственных.

Художники, работающие математиками

Устройство, симметрия, каламбуры и математика

Франсуа Морелле в своей работе постоянно вдохновлялся математикой и геометрией. Цитата с его сайта: Работы Франсуа Морелле выполняются по системе: каждый выбор определяется заранее установленным принципом. Поступая так, он хочет создать впечатление, что он контролирует художественное творчество, оставляя при этом часть шанса, которая дает непредсказуемую картину. Он использует простые формы, небольшое количество сплошных цветов и элементарные композиции (сопоставление, наложение, случайность, интерференция, фрагментация). Таким образом, он создает свои первые «рамки», сети параллельных черных линий, наложенных в определенном порядке, которые покрывают всю поверхность картин. Эти системы напоминают структуры, предложенные Oulipo (Ouvroir de Littérature Potentielle) и описанные Раймоном Кено: «Какова цель нашей работы? Предлагайте писателям новые «структуры» математического характера или даже изобретайте новые искусственные или механические процессы, способствующие литературной деятельности ». Впоследствии Франсуа Морелле продолжит использовать системы, основанные на математической вселенной.

Узлы, графики и чересстрочная развертка

Мишель Серр в своей истории геометрии объясняет, что первым математическим актом было переплетение ткачества. Мы объясняем появление математики первыми кадастровыми актами в Месопотамии или необходимостью административного учета продуктов питания и скота, археология показывает, что переплетение происходит задолго до написания, тканые структуры, играющие с узлами и переплетение, кажутся связанными с ручным управлением. способности и физическая интуиция структуры и прочности материалов. Так Мишель Серр показывает, что первый математический акт исходит из нашей способности манипулировать материалами и преобразовывать их в полезные предметы (корзины, ткани, сети и т. Д.).

Создание переплетения вызывает восхищение и развивает теоретические вопросы, которые превращают строительную игру в формальный акт. Леонардо да Винчи играл с переплетением, например, в  Кодексе Валларди,  приобретенном Лувром в 1856 году.

Леонардо да Винчи (1452-1519) из  Кодекса Валларди,  приобретенного Лувром в 1856 году у миланского антиквара Джузеппе Валларди.

Фрактальные интуиции

Пространство, нарисованное Джексоном Поллоком, было беспрецедентным в истории искусства, мы никогда не видели фракталов на картинах. Продолжая в первые годы своего существования подход современного художника по образцу подхода Пабло Пикассо , он постепенно отошел от своего желания создать поистине североамериканское живописное пространство, вдохновленное идеями Карла Юнга о коллективных мифах и психологии. Джексон Поллок обладал интуицией скалярная сложность, связанная с ландшафтом Северной Америки. Далеко от работы на основных математических понятий фракталов тогда заявленных Георга Кантора , Анри Пуанкаре . Интуиция художника подводит его к порогу небывалой концепции пространства. Эта работа выполнена с особой тщательностью, и его работы проникнуты интуицией пространства в повторяющихся масштабах. Настолько, что математики, работающие над его пространствами, находят повторения и структуры.

Кэтрин Джонс-Смит, Харш Матур и Лоуренс М. Краусс, 2008 г.

Причудливые топологии и морфология

Как понять топологические преобразования героев мультфильмов? Подобно составным созданиям из работ Жоана Миро, мультфильмы дают нам возможность непрерывно или иногда прерывисто наблюдать странную пластичную и трансформируемую фауну. Иногда персонажей обрезают, чтобы воссоздать себя, экспериментируя с правилами топологии.

N-мерные пространства, неевклидовы геометрии

В XIX — м  веке, труды Гаусса, Римана Lobatechevsky и популяризировать идею пространственных размеров и экзотических геометрий. Альберт Эйнштейн, развивая теорию относительности, предлагает культивируемой публике новые парадигмы наблюдения, которые используют некоторые художники, чтобы найти другие способы репрезентации, идея пространства-времени плодотворна, а молодые Брак и Пикассо слышат о пространстве это было бы уже не евклидовым, а сферическим или гиперболическим. Это провоцирует воображение и предлагает новые режимы описания , которые мы находим в обнаженном Спускаясь по лестнице Марселя Дюшана и в учредительном работах Брака и Пикассо аналитического кубизма , полученном в Бато Lavoir в течение первого десятилетия 20 — го века. Го  век. Такая конструкция пространства будет воплощена в фундаментальной работе в истории искусства в XX — го  столетия компания «девицы d’Avignon».

В поисках связи

К тому, чтобы обнаруживать связи между математикой и искусством, в какой-то мере подталкивали практические потребности. К примеру, на Западе сочиненные с помощью компьютера мелодии передаются по радио и записываются, а машинная графика играет весьма большую роль в оформлении книг и в прикладном искусстве — главным образом в дизайне.

Но, скажем, серьезный интерес к искусству классика американской математики Д. Биркгофа, автора опубликованной еще в 30-х годах монографии «Эстетические измерения», или одного из корифеев математики Андрея Николаевича Колмогорова, неоднократно читавшего студентам-математикам курс математических методов поэтики, связан вовсе не с соображениями практической пользы, а с тем, что изучение с помощью точных наук закономерностей искусства открывало этим выдающимся ученым нечто новое в самой математике. Особенно легко видеть это в случае А. Н. Колмогорова, поскольку идущая от него чисто математическая концепция информации, безусловно связана с размышлениями над проблемами искусства.

Обратным примером тяготения к математике человека искусства может служить творчество знаменитого голландского «математического графика» Маурица Корнелиса Эсхера, причем оказавшийся совершенно неожиданным и для самого художника успех, которым стало пользоваться его творчество, доказал совпадение его устремлений с какими-то потребностями времени.

С 1968 года издается специализированный международный журнал «Леонардо», посвященный вопросам машинного искусства и математическим подходам к искусству; в этом журнале (много внимания, кстати сказать, уделяющем творчеству Эсхера) наряду с искусствоведами и художниками, инженерами и программистами систематически участвует и ряд видных математиков.

Архитектура и математика

(Нестандартные архитектуры и нурбы )

1. Нестандартная архитектура родилась из технических возможностей, предлагаемых новейшими компьютерными инструментами, программным обеспечением для компьютерной графики 3ds Max, Rhino и его подключаемыми модулями Grasshopper, которые делают возможным процедурный морфогенез в дизайне и архитектуре. Производственная линия между дизайном и производством позволила персонализировать элементы, тем самым освободив архитектурное письмо и приблизив его к скульптуре и рисунку, но также позволив разрабатывать сложные формы, схемы которых строго документируются и выполняются в серии промышленных операций, упрощенных станками. В 1969 году инженер Безье разработал в Renault алгоритм управления эллиптическими кривыми, разработанный на основе квадратных уравнений, чтобы спроектировать кузов Renault 16. Это нововведение открыло дизайнерам возможности манипулировать эллиптическими кривыми в больших масштабах. Ранее эти методы были эмпирическими, основанными на опыте производителей котлов, которые формировали корпуса лодок или конструкции самолетов.
2. Использование кривых Безье в дизайне / биодизайне

Лента Мебиуса

Лента Мебиуса — это трехмерный объект, имеющий только одну сторону. Такая лента может быть легко получена из полоски бумаги, перекрутив один из концов полоски, а затем склеив оба конца друг с другом. Лист Мёбиуса служил вдохновением для скульптур и для графического искусства. Эшер  был одним из художников, кто особенно любил его и посвятил несколько своих литографий этому математическому объекту. Одна из известных — «Лист Мёбиуса II» показывает муравьёв, ползающих по поверхности ленты Мёбиуса. (приложение 6). Эшер изобразил ленту Мебиуса на работах «Всадники» (1946)  и «Узлы» (1965).

 Фракталы

Фрактал — это объект, повторяющий сам себя в различных масштабах, которые связаны математическим способом.  К сожалению, фракталы как таковые были недоступны Эшеру, потому что были формализованы и выделены в отдельную область математики лишь после его смерти. Эшер очень интересовался изображением бесконечного в пределах конечной области, в частности бесконечными тесселляциями. Ниже приведены примеры современных художников Кэри Митчелл  (приложение 7) и Роберта Фатауэра (приложение 8).

Математика в живописи

Также наиболее близки к традиционному «математическому искусствоведению» книги известного механика, Б. В. Раушенбаха «Пространственные построения в древнерусской живописи» и продолжающая и расширяющая ее рамки монография «Пространственные построения в живописи». Они посвящены весьма техническому и безусловно доступному математическому анализу вопросу — о средствах воспроизведения на плоскости пространственных объектов.

Обе книги Раушенбаха построены по одному плану

Основную часть занимает обращенный к широкому и не имеющему математического образования читателю искусствоведческий анализ произведений искусства с особым вниманием к системе передачи на плоскости пространственных объектов. В первой из названных книг автор в основном сравнивает систему пространственных изображений в православной иконописи и в европейской живописи, опирающейся на опыт художников и теоретиков итальянского Ренессанса; во второй отдельные главы посвящены:

• древнеегипетскому искусству;
• византийской и древнерусской иконе;
• индийской и персидской миниатюре;
• живописи Поля Сезанна.

Этот сравнительный разбор произведений искусства, проведенный заинтересованным и внимательным наблюдателем, обращен ко всем любителям живописи, в том числе и к тем из них, которые полностью чужды математики,— мало кого оставит равнодушным сопоставление изобразительных эффектов прямой и обратной перспективы в первой книге Раушенбаха или анализ пространственных построений Сезанна во второй его книге. Я даже подозреваю, что раскупили обе книги Раушенбаха в первую очередь именно чуждые математики читатели — в силу их многочисленности.

Однако рассчитаны эти книги, прежде всего, безусловно, не на них. Большую роль в системе авторской аргументации играют заключающие обе книги математические приложения «Наброски теории пространственных построений в изобразительном искусстве», ради которых, в значительной степени, были и написаны книги. Эти приложения содержат математическую теорию искаженной или криволинейной («прецептивной» по терминологии автора) перспективы, объясняющую многие особенности изображения. Такая перспектива учитывает эффект бинокулярного зрения, игнорируемый линейной перспективой.

Фрактал

@stevenlasry / unsplash.com

Фракталы – это множество, которое обладает свойствами самоподобия. К примеру, вы можете увидеть капусту сорта Романеско – один из самых распространенных фракталов в нашей повседневной жизни. По сути, если рассмотреть кочан Романеско в крупном масштабе, то каждый мелкий фрагмент будет иметь форму этого самого кочана. 

YouTube, канал

Такие фрактальные структуры встречаются повсюду. Снежные кристаллы, побережья, облака, речные потоки, цветы, кроны деревьев и кровеносные сосуды – все это может обладать свойствами фрактала.

phys.org

И если в природе фрактальный слой имеет конец, то в концептуальном плане он бесконечен. «Если вы создадите фрактальную фигуру на компьютере, то не сможете увидеть конец фрактала, независимо от того, насколько вы увеличите масштаб», – отметил Бриц.

Число «π»

img.buzzfeed.com

Если говорить коротко, то «π» намного больше, чем 3,14, к которому мы привыкли. «Число «π» используется при расчете длины и площади окружности круга, но на самом деле его свойства куда шире», – утверждает Блиц.

«Если вы посмотрите на все, что вас окружает, вы сможете найти «π» практически повсеместно. Оно появляется не только там, где есть связь с кругом, но и в формулах вероятности и исчисления, которые не имеют ничего общего с круглой формой», – заявляет Томас.

Несмотря на то что о «π» знает каждый, это одно из самых тайных чисел! Это в буквальном смысле бесконечная периодическая дробь. В 2016 году швейцарский ученый Петер Трюб определил до 22,4 триллиона знаков после запятой. Интересен и тот факт, что цифры не складываются в повторяющиеся блоки, поэтому, теоретически, в числе «π» вы можете найти свой номер телефона.

Эта загадка числа «π» еще раз придает математике особую красоту и очарование.

С чего все начиналось

Художники античности практически не прибегали к использованию перспективы

Вместо правильного изображения объектов на плоскости творцы выделяли более тематически значимые предметы и привлекали внимание к определенным фигурам

Начиная с эпохи Возрождения, математика все больше затрагивала сферы изучения природы и искусства. С этим связана и заинтересованность художников точной наукой. Во-первых, они хотели добиться правильного размещения объектов на рисунке. Во-вторых, многие философы и деятели искусств верили, что математика — истинная суть мира, и все подчинено геометрическим законам.

Итальянский художник и архитектор эпохи Проторенессанса Джотто ди Бондоне был одним из первых, кто начал применять законы перспективы в работах.

Золотое сечение

Если говорить научным языком, то золотое сечение — это отношение между частями целого, при котором меньшее относится к большему так же, как и большее к целому.

Присмотревшись к «золотой спирали» ближе, можно заметить, что ее структура напоминает ряд чисел Фибоначчи — последовательность, где каждое следующее число равно сумме двух предыдущих:

0, 1, 1, 2, 3, 5, 8, 13, 21, 34, 55…

Так как изобразить ноль графически нельзя, рисование начинается с квадрата со стороной 1.

Для более гармоничной композиции правило золотого сечения применяют в живописи, фотографии, дизайне, архитектуре, скульптуре и даже музыке. Пропорция позволяет выстроить объекты правильно с точки зрения эстетики.

В картинах

Леонардо да Винчи применял золотое сечение в своем творчестве наиболее часто. Также именно он продемонстрировал связь между человеческим телом и Божественной пропорцией.

Золотое сечение задает направление художникам, указывает, где должны располагаться первостепенные и второстепенные фигуры, помогает создать композицию. Но Архимедову спираль, которую мы продемонстрировали выше, можно наблюдать в картинах не всегда. Творцы пользуются и другими принципами сечения:

На картинке выше можно наблюдать упрощенное правило золотого сечения, «правило третей». Изображение условно делится на 3 части по горизонтали и вертикали, образуя 9 ячеек и 4 точки пересечения по центру

Именно эти точки привлекают человеческий глаз в первую очередь, и только после того как мы взглянем на них, обращаем внимание на остальные предметы картины

Узнать больше о золотом сечении и о том, как развивалась идея, можно из видео:

Рождение воображаемого числа и умение изобрести устойчивую форму

Этот раздел может содержать неопубликованные работы или непроверенные заявления  (март 2021 г.) . Вы можете помочь, добавив ссылки или удалив неопубликованный контент.

Появление числа i вызвало землетрясение в математической мысли, запретный, невообразимый объект, он приобрел стабильные и повторяющиеся свойства, чтобы наконец стать эффективным инструментом расчета, допускающим множество концептуальных и практических новшеств. Эта концептуальная открытость подобна стилистическим революциям, когда то, что когда-то было невидимым, становится невидимым после его распространения в современной культуре. Площади белый на белом фоне с Малевич протекает таким же образом , как парадигматическая революцию. Белая поверхность, которая была тривиальной, использованная определенным образом, производит сильный знак в метафизике ее наблюдателя.

Искаженные и необычные перспективы

Необычные системы перспективы, содержащие две или три исчезающие точки, также являются
излюбленной темой многих художников. К ним также относится родственная область —
анаморфное искусство. Эшер использовал искаженную перспективу в нескольких своих работах
«Наверху и внизу» (1947), «Дом лестниц» (1951) и
«Картинная галерея» (1956).
Дик Термес (Dick Termes) использует шеститочечную перспективу для рисования сцен на
сферах и многогранниках, как показано на примере ниже.

Dick Termes «Клетка для человека» (1978). Это разукрашенная сфера, в процессе
создания которой использовалась шеститочечная перспектива. На ней изображения
геометрическая структура в виде сетки, сквозь которую виден ландшафт.
Три ветки проникают внутрь клетки, а также по ней ползают рептилии.
В то время как одни изучают мир, другие обнаруживают себя, находящимися в клетке.

Слово анаморфный (anamorthic) сформировано из двух греческих слов «ana» (снова) и
morthe (форма). К анаморфным относятся изображения настолько сильно искаженные, что
разобрать их без специального зеркала бывает невозможно. Такое зеркало иногда
называют анаморфоскопом. Если смотреть в анаморфоскоп, то изображение
«формируется снова» в узнаваемую картину. Европейские художники раннего Ренессанса
были очарованы линейными анаморфными картинами, когда вытянутая картина становилась
снова нормальном при обзоре под углом. Известный премер — картина Ханса Хольбейна (Hans Holbein)
«Послы» («The Ambassadors») (1533), в которой изображен вытянутый череп.
Картина может быть наклонена в верхней части лестницы так, что люди, поднимающиеся
по лестнице будут напуганы изображением черепа. Анаморфные картины, для просмотра
которых необходимы цилиндрические зеркала, были популярны в Европе и на Востоке
в XVII-XVIII веках. Часто такие изображения несли сообщения политического протеста
или были эротического содержания. Эшер не использовал в своей работе классические
анаморфные зеркала, однако, в некоторых своих картинах он использовал сферические
зеркала. Самая известная его работа в этом стиле «Рука с отражающей сферой» (1935).
Пример ниже показывает классическое анаморфное изображение работы Иштвана Ороса (Isvan Orosz).

Istvan Orosz «Колодец» (1998). Картина «Колодец» полученая печаться с гравюры
по металлу. Работа была создана к столетию со дня рождения М.К. Эшера.
Эшер писал об экскурсиях в математическое искусство, как о прогулся
по прекрасному саду, где ничто не повторяется. Ворота в левой части картины
отделяют эшеровский математический сад, находящийся в мозге, от
физического мира. В разбитом зеркале в правой части картины
присутствует вид маленького городка Атрани (Atrani) на побережье Амалфи (Amalfi) в Италии.
Эшер любил это место и прожил там некоторое время. Он изобразил этот
город на второй и третьей картинах из серии «Метаморфозы». Если поместить
цилиндрическое зеркало на место колодца, как это показано справа, то в нем,
как по волшебству, появится лицо Эшера.

Математика и дизайн интерьера

Очень важно при планировании дизайна точно определить, какую мебель выбрать (вид и размер мебели). Тут без математики не обойтись

Дизайнеры интерьеров должны уметь измерять пространство, которое они собираются заполнять. Значение имеет и размер мебели. Маленькие ретро-стулья могут выглядеть великолепно, но если они «потеряются» в большом помещении, то их красота уже не будет иметь значения.

Без надлежащих измерений потолка, полов и стен комната не может быть украшена надлежащим образом. И не всегда визуальное восприятие может сработать так, чтобы все в комнате было оформлено на «ура». А потому дизайнеры (не декораторы) интерьеров должны уметь читать и делать чертежи и/или уметь создавать свои проекты в 3D проекции.

Дизайнер при разработке своего проекта должен учитывать бюджет заказчика и соответственно рассчитывать стоимость проекта, начиная от отделочных материалов до аксессуаров. А также уметь высчитать сроки работ, что тоже будет влиять не только на гонорар, но и дальнейшую оценку его как профессионала.

Дизайн интерьера — не только красота и гламур, но и необходимые знания по компьютерной графике, математическому моделированию,  геометрии, механике, черчению, тригонометрии и арифметике, а также других основ математики. Отсюда следует вывод — дизайну просто не обойтись без математики. Факт, известный еще древним египтянам, римлянам, инкам… И современным дизайнерам.

Не только архитектура

Не только в архитектуре и искусстве, но и в интерьере мы можем увидеть «работу» математики. Вспомните, что мы с вами уже знаем о балансе. Моделирование и планирование пространства интерьера не обходится без баланса (симметрии, асимметрии, радиальности)…

Фракталы

Фракталы — математические последовательности (самоподобные множества) — еще один прием математики, используемый дизайнерами. Фракталы повторяют геометрические узоры, которые объединяются для создания единого целого.

Дизайнеры используют фракталы для оригинального дизайна комнаты. Будь то рисунок на обоях или оформление всего интерьера.

А как обойтись без фракталов, когда создаются украшения к празднику? Например, к Новому году. Снежинки, вырезанные из бумаги или объемные оригами для герлянды… Разве это не пример дизайна интерьера и в то же время математики?

Симметрия

@vincentvanzalinge / unsplash.com 

В своем выступлении «Математические эмоции» на TEDxUNSWSydney в 2018 году Томас Бриц рассказал, что мы испытываем восторг, радость и удивление не только, когда видим красоту в окружающих нас вещах – людях, фотографиях, фильмах, пейзажах, предметах высокого искусства, – но и красоту в математике.

Когда мы замечаем симметрию и определенные шаблоны, приходим к неожиданному решению или разгадываем математическую головоломку.

Уверены, каждому из нас хорошо знакомо понятие симметрии, которая часто встречается в нашей жизни. Зачастую предметам, созданным руками человека, намеренно придается симметричная форма, потому что так изделие будет выглядеть приятнее для человеческого глаза.

Канал YouTube ()

«Так сложилось, что нам симпатично более симметричное лицо, – объяснил Томас. – Но немного хаоса и уникальных черт не сделают его несовершенным. Они сделают его более очаровательным для нашего восприятия».

Симметрия широко встречается и в природе. Если провести посередине тела человека вертикальную линию, левая сторона будет почти симметрична правой. Симметрией обладают снежинки, кристаллы, падающие дождевые капли, которые имеют форму сферы, и многое другое.

Многогранники

Многогранник — это трехмерное тело, гранями которого являются многоугольники. Существует всего пять правильных многогранников, у которых все стороны являются правильными многоугольниками и все вершины одинаковы. Они известны как многоугольники Платона или Платоновы тела. Также существует 13 выпуклых многогранников, гранями которых являются один, два или три правильных многоугольника, и у которых все вершины одинаковы. Они известны как тела Архимеда. Кроме этого существует бесконечное множество призм и антипризм с гранями в виде правильных многоугольников. М. К. Эшер использовал многогранники во многих своих работах, включая «Рептилии» (1949) (приложение 5). Впервые работа была напечатана в марте 1943 года.

На ней изображен стол, с расположенными на нем предметами и рисунком рептилий собранных в виде мозаики. Рептилии оживают, ползают по кругу по предметам расположенным на столе и в конечном итоге возвращаются обратно в плоский рисунок. На столе расположены обычные предметы — книги (та, по которой ползёт рептилия — учебник по зоологии), посуда, горшок с цветами, среди них выделяется металлический додекаэдр на который рептилии поднимаются. Ящерицы маленького размера, но не кажутся безобидными, имеют настоящие клыки. Одна из рептилий, сидящая на грани додекаэдра, выпускает пар из ноздрей.

Тесселляции

Тесселляции, известные также как покрытие плоскости плитками (tiling), являются коллекциями
фигур, которые покрывают всю математическую плоскость, совмещаясь друг с другом без наложений и пробелов.
Правильные тесселляции состоят из фигур в виде правильных многоугольников, при совмещении которых
все углы имеют одинаковую форму. Существует всего три многоугольника, пригодные для использования
в правильных тесселляциях. Это — правильный треугольник, квадрат и правильный шестиугольник.
Полуправильными тесселляциями называют такие тесселляции, в которых использованы правильные многоугольники
двух или трех типов и все вершины одинаковы. Существует всего 8 полуправильных тесселляций.
Вместе три правильных тесселляции и восемь полуправильных носят название Архимедовых.
Тесселляции, в которых отдельные плитки являются узнаваемыми фигурами, являются одной из основных
тем творчества Эшера. В его записных книгах содержатся более 130 вариантов тесселляций. Он
использовал их в огромном количестве своих картин, среди которых «День и ночь» (1938), серия картин
«Предел круга» I-IV, и знаменитые «Метаморфозы» I-III (1937-1968). Примеры ниже — картины современных
авторов Холлистера Девида (Hollister David) и Роберта Фатауэра (Robert Fathauer).

Hollister David «Семь птиц». На этой картине изображены семь птиц, две из которых
изображены в негативе на фоне ландшафта города Ахо в Аризоне. Последовательно
уменьшающиеся фигуры птиц совмещаются друг с другом в виде фрактальной тесселляции.
Хвостовые перья каждой птицы являются разделяют конструкцию напополам, отсекая примерно треть
расстояния между кончиками крыльев. Каждая меньшая птица в свою очередь делит свою область
аналогичным образом. Если этот процесс продолжать до бесконечности, получится набор
точек, известный как множество Кантора или Канторова пыль.

Robert Fathauer «Фрактальные рыбы — сгруппированные группы».
Это компьютерная работа, распечатанная на фотобумаге.
Сквозь иллюминатор видны волны, но при ближайшем рассмотрении видно,
что волны являются на самом деле фрактальной тесселляцией, состоящей из рыб.

Приложения

На французском

• Марсель Бергер , Живая геометрия или шкала Якоба, Кассини, колл. «Новая математическая библиотека», 2009 г. ( ISBN  978-2-84225035-5 )
• Мишель Серр Истоки геометрии, дата публикации май 201, Collection Champs Sciences, номер 331, формат 11 см x 18 см, ( ISBN   )
• Рене Том, Локальное и глобальное в произведении искусства, страсть к формам (Рене Тому), работа 1 и 2, коллекция Theoria, ENS éditions, Fontenay Saint Cloud, коллективная работа под редакцией Мишеля Порте, 1994, ( ISBN   ) см Le Деба, п о  24, март 1983, ( ISSN   )
• Словарь геометрии для архитектуры, Паскаль Терракол , Издания
• Топологические эксперименты, Стивен Барр, коллекция Lysimachus, Belin Diffusion, ( ISBN  2-7011-1108-0 )
• Фигуры бесконечности, Тони Леви , éditions du Seuil, 1987, ( ISBN  2-02-009609-9 )
• Фредерик Мигайру , Нестандартные архитектуры , Editions du Center Pompidou, 3 декабря 2003 г. ( ISBN   и 978-2844262318 )

На английском

• (о) Клод Bruter ( реж. ), Математика и современное искусство (Труды Первого ЭСМА  (еп) конференция, состоявшийся в Париже 19-22 июля 2010 года), Springer, сб.  «Шпрингер Труды по математике» ( п о  18),2012 г.( ISBN  978-3-642-24496-4 , DOI   )
• Пугающая симметрия, Ян Стюарт и Мартин Голубицкий , (Играет ли Бог в кости?), 1992, Blackwell Publishing Oxford UK и Cambridge USA, ( ISBN   )
• Книга топологических изображений, Georges K. Francis , Springer verlag 1987, ( ISBN   и )
• О росте и форме, Дарси Томпсон , Кембриджская наука в мягкой обложке, 1961 г. ( ISBN   ).
• Fractal for the classroom, Ouvrage коллектив, Хайнц-Отто Пайтген , Хармут Юргенс , Дитмар Саупе , Springer Verlag New York, Национальный совет учителей математики, 1991, ( ISBN  0-387-97041-X и 3-540-97041-X )
• Кривые жизни, Теодор Андреа Кук, 1979, издательство Dover, ( ISBN  0-486-23701-X )
• Визуальный разум: искусство и математика, RODIN, Ervin Y, EditionEMMER, Michele; 1993 г.

  Резюме :

  Сборник эссе о взаимосвязи искусства и математики, написанных математиками, интересующимися визуальными аспектами своих вычислений, и художниками, интересующимися математическим происхождением и вдохновением их работ. Включает разделы по геометрии и визуализации; компьютерная графика, геометрия и искусство; симметрия; и перспектива, математика и искусство. ;

  ИНИСТ (24889824), ( ISBN  026205048X )

• ; Словарь геометрии для архитектуры Онтологии для моделей синтеза, Pascal TERRACOL, Париж: Presse des Ponts, 2017, Модель: ISBN: 978-2-85978-509-3, 2017

Невозможные фигуры

Невозможные фигуры — эти фигура, изображенная в перспективе таким способом, чтобы выглядеть на первый взгляд обычной фигурой. Однако при более внимательном рассмотрении зритель понимает, что такая фигура не может существовать в трехмерном пространстве. М. К. Эшер изобразил невозможные фигуры на своих известных картинах «Бельведер» (1958), «Восхождение и спуск»(1960) и «Водопад» (1961) (приложение 3). Одним из примеров невозможной фигуры служит картина современного венгерского художника Иштвана Ороса «Перекрестки» (1999) (приложение 4). Репродукция гравюры по металлу. На картине изображены мосты, которые не могут существовать в трехмерном пространстве. Например, есть отражения в воде, которые не могут быть исходными мостами.